algorithm

基本概念

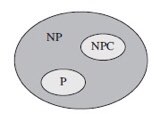
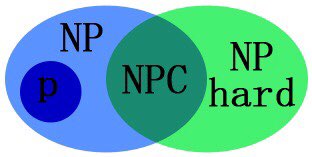
1. P问题：能够在多项式时间内解决的决策问题。

2. NP问题：多项式时间内能够验证的问题称为NP问题。

3. NPC问题：可以在多项式时间内对问题所有可能的解进行验证,并给出其正确性的问题。目前不能用多项式时间解决，但还不能证明这个问题不能用多项式解决。
   规约（Reduction）：如果要证明一个问题是NPC问题，则只需要证明他是NP问题，然后找一个你所知道的NPC问题规约到A即可。

4. NP-hard问题：是指从算法角度比NP还难的问题，指的是所有的NP问题可以通过某个多项式时间的函数规约到这类问题。NP-hard问题不一定是NP问题，因为总有一些NP-hard问题无法在多项式时间判断一个解是否可行。

5. 如果A到B规约成功，则说明：B至少比A要难，即只要有一个解决B的黑盒子算法，就能解决A问题。
   故在证明一个问题是NPC问题时，如果掌握的已知NPC问题越多，对于规约越有利。

6. 一般来说证明B是NPC的过程如下：

   1. 证明B是NP问题。
   2. 知道一个已知的NPC问题A。
   3. 给出一个规约过程A规约到B，并证明此规约过程是多项式时间的。
      
      

7. 独立集：一个点集，点集中各点没有关系。（点独立）

8. 最大独立集：点的个数最多的独立集。最大独立集 == 点的总数 - 最小点覆盖。

9. 最小点覆盖：图中每个边至少一个端点在该点集中的最小点集。（点覆盖所有边)

点覆盖规约到集合覆盖：

Boolean satisfiability problem 简称SAT，简单说就是用来判断一组给定的布林函数，是否可以找到一组变数赋值能使其为真。SAT是第一个NP-Complete problem

SAT规约到3-SAT：

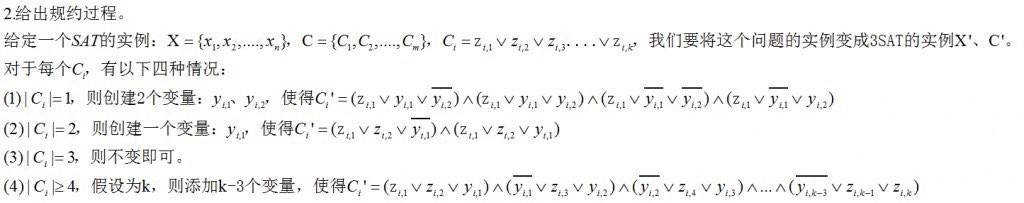
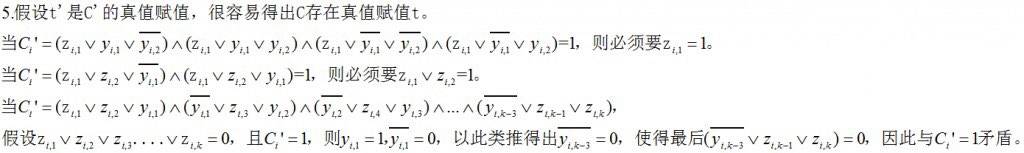
3-SAT规约到独立集：

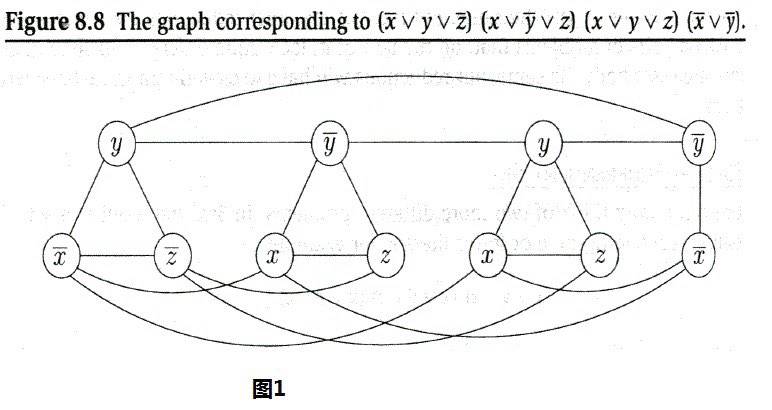
3-SAT规约到点覆盖：

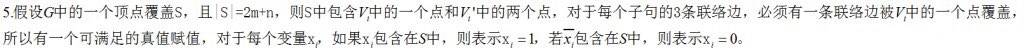
哥尼斯堡七桥问题是在寻找一条遍历图中所有边的简单路径，而哈密尔顿的周游世界问题则是在寻找一条遍历图中所有点的基本路径。

CIRCUIT-SAT规约到SAT

3-SAT规约到有向哈密尔顿回路：

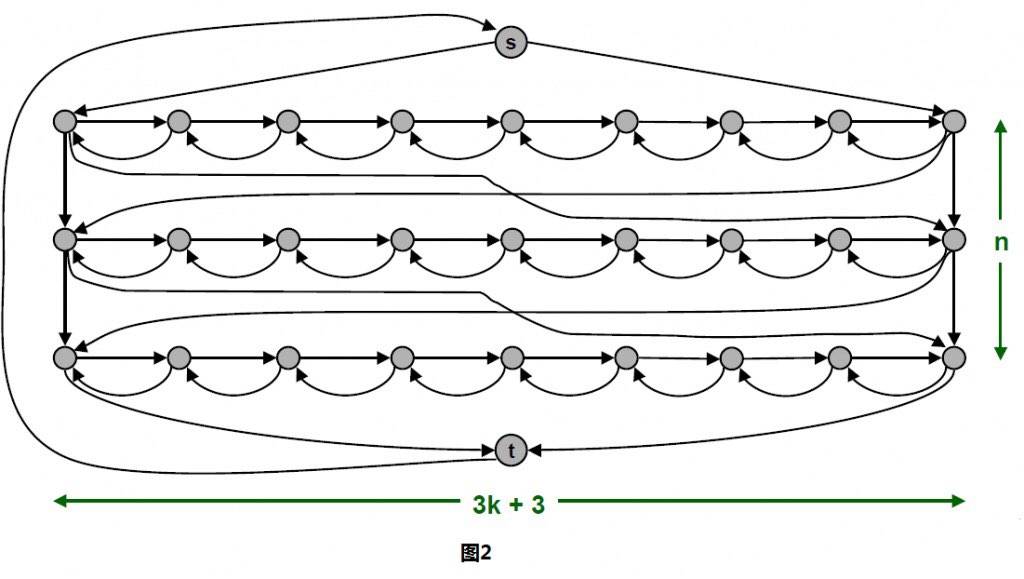
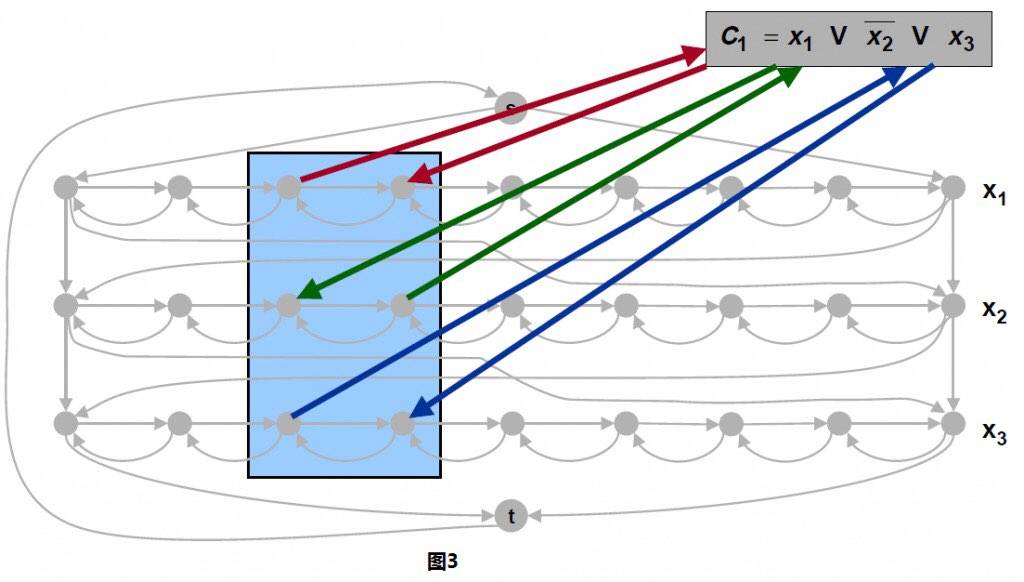
汉密尔顿路径规约到汉密尔顿回路：

汉密尔顿回路规约到汉密尔顿路径：

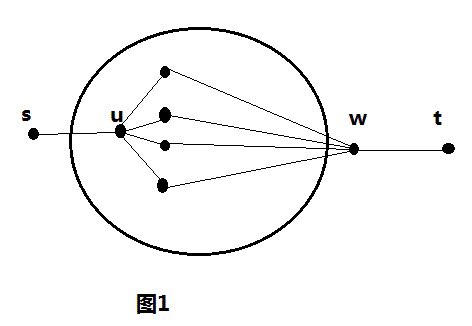
有向汉密尔顿回路规约到无向汉密尔顿回路：

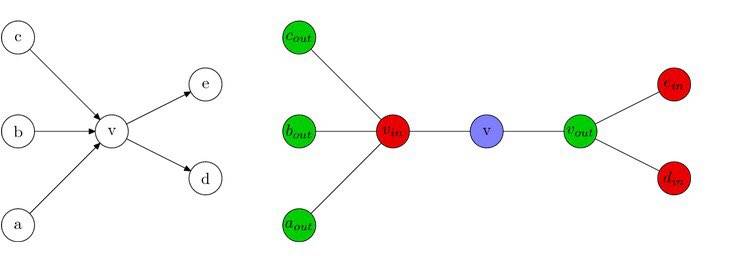
无向汉密尔顿回路规约到有向汉密尔顿回路：

图片证明来自网络。